- Pembuatan atau penulisan algoritma tidak tergantung pada bahasa pemrograman manapun, artinya penulisan algoritma independen dari bahasa pemrograman dan komputer yang melaksanakannya.
- Notasi algoritma dapat diterjemahkan ke dalam berbagai bahasa pemrograman.
- Apapun bahasa pemrogramannya, output yang akan dikeluarkan sama karena algoritmanya sama.
- Teks algoritma berisi deskripsi langkah-langkah penyelesaian masalah. Deskripsi tersebut dapat ditulis dalam notasi apapun asalkan mudah dimengerti dan dipahami.
- Tidak ada notasi yang baku dalam penulisan teks algoritma seperti notasi bahasa pemrograman. Notasi yang digunakan dalam menulis algoritma disebut notasi algoritmik.
- Setiap orang dapat membuat aturan penulisan dan notasi algoritmik sendiri. Hal ini dikarenakan teks algoritma tidak sama dengan teks program. Namun, supaya notasi algoritmik mudah ditranslasikan ke dalam notasi bahasa pemrograman tertentu, maka sebaiknya notasi algoritmik tersebut berkorespondensi dengan notasi bahasa pemrograman secara umum.
- Notasi algoritmik bukan notasi bahasa pemrograman, karena itu pseudocode dalam notasi algoritmik tidak dapat dijalankan oleh komputer. Agar dapat dijalankan oleh komputer, pseudocode dalam notasi algoritmik harus ditranslasikan atau diterjemahkan ke dalam notasi bahasa pemrograman yang dipilih. Perlu diingat bahwa orang yang menulis program sangat terikat dalam aturan tata bahasanya dan spesifikasi mesin yang menjalannya.
- Algoritma sebenarnya digunakan untuk membantu kita dalam mengkonversikan suatu permasalahan ke dalam bahasa pemrograman.
- Algoritma merupakan hasil pemikiran konseptual, supaya dapat dilaksanakan oleh komputer, algoritma harus ditranslasikan ke dalam notasi bahasa pemrograman. Ada beberapa hal yang harus diperhatikan pada translasi tersebut, yaitu :
- Mengerti setiap langkah dalam algoritma.
- Mengerjakan operasi yang bersesuaian dengan langkah tersebut.
- Bahasa pemrograman bertujuan khusus. Yang termasuk kelompok ini adalah Cobol (untuk terapan bisnis dan administrasi). Fortran (terapan komputasi ilmiah), bahasa rakitan (terapan pemrograman mesin), Prolog (terapan kecerdasan buatan), bahasa-bahasa simulasi, dan sebagainya.
- Bahasa perograman bertujuan umum, yang dapat digunakan untuk berbagai aplikasi. Yang termasuk kelompok ini adalah bahasa Pascal, Basic dan C. Tentu saja pembagian ini tidak kaku. Bahasabahasabertujuan khusus tidak berarti tidak bisa digunakan untuk aplikasi lain. Cobol misalnya, dapat juga digunakan untuk terapan ilmiah, hanya saja kemampuannya terbatas. Yang jelas, bahasabahasa pemrograman yang berbeda dikembangkan untuk bermacam-macam terapan yang berbeda pula.
- Bahasa tingkat rendah. Bahasa jenis ini dirancang agar setiap instruksinya langsung dikerjakan oleh komputer, tanpa harus melalui penerjemah (translator). Contohnya adalah bahasa mesin. CPU mengambil instruksi dari memori, langsung mengerti dan langsung mengerjakan operasinya. Bahasa tingkat rendah bersifat primitif, sangat sederhana, orientasinya lebih dekat ke mesin, dan sulit dipahami manusia. Sedangkan bahasa rakitan dimasukkan ke dalam kelompok ini karena alasan notasi yang dipakai dalam bahasa ini lebih dekat ke mesin, meskipun untuk melaksanakan instruksinya masih perlu penerjemahan ke dalam bahasa mesin.
- Bahasa tingkat tinggi, yang membuat pemrograman lebih mudah dipahami, lebih “manusiawi”, dan berorientasi ke bahasa manusia (bahasa Inggris). Hanya saja, program dalam bahasa tingkat tinggi tidak dapat langsung dilaksanakan oleh komputer. Ia perlu diterjemahkan terlebih dahulu oleh sebuah translator bahasa (yang disebut kompilator atau compiler) ke dalam bahasa mesin sebelum akhirnya dieksekusi oleh CPU. Contoh bahasa tingkat tinggi adalah Pascal, PL/I, Ada, Cobol, Basic, Fortran, C, C++, dan sebagainya.
- Tingkat kepercayaannya tinggi (realibility). Hasil yang diperoleh dari proses harus berakurasi tinggi dan benar.
- Pemrosesan yang efisien (cost rendah). Proses harus diselesaikan secepat mungkin dan frekuensi kalkulasi yang sependek mungkin.
- Sifatnya general. Bukan sesuatu yang hanya untuk menyelesaikan satu kasus saja, tapi juga untuk kasus lain yang lebih general.
- Bisa dikembangkan (expandable). Haruslah sesuatu yang dapat kita kembangkan lebih jauh berdasarkan perubahan requirement yang ada.
- Mudah dimengerti. Siapapun yang melihat, dia akan bisa memahami algoritma Anda. Susah dimengertinya suatu program akan membuat susah di-maintenance (kelola).
- Portabilitas yang tinggi (portability). Bisa dengan mudah diimplementasikan di berbagai platform komputer.
- Precise (tepat, betul, teliti). Setiap instruksi harus ditulis dengan seksama dan tidak ada keragu-raguan, dengan demikian setiap instruksi harus dinyatakan secara eksplisit dan tidak ada bagian yang dihilangkan karena pemroses dianggap sudah mengerti. Setiap langkah harus jelas dan pasti.
- Jumlah langkah atau instruksi berhingga dan tertentu. Artinya, untuk kasus yang sama banyaknya, langkah harus tetap dan tertentu meskipun datanya berbeda.
- Efektif. Tidak boleh ada instruksi yang tidak mungkin dikerjakan oleh pemroses yang akan menjalankannya.
- Harus terminate. Jalannya algoritma harus ada kriteria berhenti. Pertanyaannya adalah apakah bila jumlah instruksinya berhingga maka pasti terminate?
- Output yang dihasilkan tepat. Jika langkah-langkah algoritmanya logis dan diikuti dengan seksama maka dihasilkan output yang diinginkan.
- Input: algoritma dapat memiliki nol atau lebih inputan dari luar.
- Output: algoritma harus memiliki minimal satu buah output keluaran.
- Definiteness (pasti): algoritma memiliki instruksi-instruksi yang jelas dan tidak ambigu.
- Finiteness (ada batas): algoritma harus memiliki titik berhenti (stopping role).
- Effectiveness (tepat dan efisien): algoritma sebisa mungkin harus dapat dilaksanakan dan efektif. Contoh instruksi yang tidak efektif adalah: A = A + 0 atau A = A * 1
- Flowchart sistem yaitu bagan dengan simbol-simbol tertentu yang menggambarkan urutan prosedur dan proses suatu file dalam suatu media menjadi file di dalam media lain, dalam suatu sistem pengolahan data. Beberapa contoh Flowchart sistem:
- Flowchart program yaitu bagan dengan simbol-simbol tertentu yang menggambarkan urutan proses dan hubungan antar proses secara mendetail di dalam suatu program.
- Input,
- Proses pengolahan dan
- Output
- START, berisi pernyataan untuk persiapan peralatan yang diperlukan sebelum menangani pemecahan persoalan.
- READ, berisi pernyataan kegiatan untuk membaca data dari suatu peralatan input.
- PROSES, berisi kegiatan yang berkaitan dengan pemecahan persoalan sesuai dengan data yang dibaca.
- WRITE, berisi pernyataan untuk merekam hasil kegiatan ke peralatan output.
- END, mengakhiri kegiatan pengolahan.
- Hindari pengulangan proses yang tidak perlu dan logika yang berbelit sehingga jalannya proses menjadi singkat.
- Jalannya proses digambarkan dari atas ke bawah dan diberikan tanda panah untuk memperjelas.
- Sebuah flowchart diawali dari satu titik START dan diakhiri dengan END.
- Simbol pertama menunjukkan dimulainya sebuah program.
- Simbol kedua menunjukkan bahwa input data dari p dan l.
- Data dari p dan l akan diproses pada simbol ketiga dengan menggunakan perumusan L = p. l.
- Simbol keempat menunjukkan hasil output dari proses dari simbol ketiga.
- Simbol kelima atau terakhir menunjukkan berakhirnya program dengan tanda End.
- Struktur Runtunan
- Digunakan untuk program yang pernyataannya sequential atau urutan.
- Struktur Pemilihan
- Digunakan untuk program yang menggunakan pemilihan atau penyeleksian kondisi.
- Struktur Perulangan
- Digunakan untuk program yang pernyataannya akan dieksekusi berulang-ulang.
- Masukkan bilangan pertama
- Masukkan bilangan kedua
- Jika bilangan pertama > bilangan kedua maka kerjakan langkah 4, jika tidak, kerjakan langkah 5.
- Tampilkan bilangan pertama
- Tampilkan bilangan kedua
- Masukkan bilangan pertama (a)
- Masukkan bilangan kedua (b)
- if a > b then kerjakan langkah 4
- print a
- print b
- Definisikan Masalah
- Buat Algoritma dan Struktur Cara Penyelesaian
- Menulis Program
- Mencari Kesalahan
- Uji dan Verifikasi Program
- Dokumentasi Program
- Pemeliharaan Program
sumber: https://andikafisma.wordpress.com/algoritma-dan-pemrograman/ Pengenalan Desain dan Analisis Algoritma
Sebagai salah satu dasar dari ilmu komputer, algoritma merupakan hal yang sangat penting untuk dikuasai oleh orang-orang yang berkecimpung di dunia ilmu komputer, dari peneliti sampai ke praktisi. Tentunya penguasaan akan algoritma tidak cukup hanya sampai pada tahap mengetahui dan menggunakan algoritma yang tepat untuk menyelesaikan masalah. Seorang yang mengerti ilmu komputer harus juga mampu merancang dan mengembangkan sebuah algoritma berdasarkan masalah-masalah yang ditemui. Tulisan ini bertujuan untuk memberikan pengertian mendasar mengenai perancangan (desain) dan pengembangan algoritma, agar pembaca dapat tidak hanya menggunakan algoritma yang sudah ada, tetapi juga merancang dan mengembangkan algoritma sesuai dengan masalah yang akan diselesaikan.
Selain memberikan dasar perancangan, tulisan ini juga membahas jenis-jenis algoritma yang ada, untuk kemudian melakukan analisa terhadap beberapa algoritma untuk setiap jenisnya. Analisis algoritma dilakukan dengan tujuan utama agar pembaca dapat mengambil keputusan yang tepat dalam memilih algoritma untuk solusi.
Apa itu Algoritma?
Sebelum membahas mengenai perancangan ataupun analisis algoritma, tentunya kita terlebih dahulu harus mendefinisikan arti dari “Algoritma”. Apa itu algoritma?
Program komputer umumnya dibangun dengan menggunakan beberapa algoritma untuk menyelesaikan sebuah permasalahan. Misalnya sebuah program pencarian teks sepertiAlgoritma merupakan langkah-langkah (prosedur) yang harus dilakukan untuk menyelesaikan sebuah masalah.grepakan memerlukan algoritma khusus untuk membaca dan menelusuri file, algoritma lain untuk mencari teks yang tepat di dalam file, dan satu algoritma lagi untuk menampilkan hasil pencarian ke pengguna.
Dalam mendefinisikan algoritma, kita harus dapat mendefinisikan tiga hal utama dengan jelas, yaitu:
- Masalah, yaitu sebuah persoalan yang ingin diselesaikan oleh sebuah algoritma.
- Masukan, yaitu contoh data atau keadaan yang menjadi permasalahan.
- Keluaran, yaitu bentuk akhir dari data atau keadaan setelah algoritma diimplementasikan ke masukan. Keluaran merupakan hasil ideal yang diinginkan dan dianggap telah menyelesaikan masalah.
Contoh (dan Solusi) Algoritma
Contoh dari sebuah definisi algoritma yang benar adalah sebagai berikut:
- Masalah
- Pengurutan sekumpulan nilai yang bernilai acak.
- Masukan
- Serangkaian data berukuran $n$.
- Keluaran
- Serangkaian data berukuran $n$, dengan urutan
a1≤a2≤a3≤...≤an−1≤an , di manaax adalah data pada posisix dalam rangkaian.
[2, 5, 1, 3, 4]ataupun["Doni", "Andi", "Budi", "Clara"]. Data keluaran yang diinginkan, tentunya adalah data masukan yang telah terurut:[1, 2, 3, 4, 5]dan["Andi", "Budi", "Clara", "Doni"].
Untuk menyelesaikan masalah yang diberikan di atas, kita dapat menggunakan algoritmainsertion sort. Kode di bawah menunjukkan implementasiinsertion sortpada bahasa pemrogramanpython:
Implementasidef insertion_sort(data): for i in range(0, len(data)): insert_val = data[i] hole_pos = i while hole_pos > 0 and insert_val < data[hole_pos - 1]: data[hole_pos] = data[hole_pos - 1] hole_pos = hole_pos - 1 data[hole_pos] = insert_val
insertion sortyang diberikan di atas menunjukkan bahwa pada dasarnya sebuah prosedur yang harus dijalankan untuk mengubah data masukan menjadi data keluaran, sehingga masalah dapat terselesaikan.
Algoritma yang Baik
Kita telah mengetahui dengan jelas makna dari algoritma, sehingga pertanyaan selanjutnya adalah algoritma seperti apa yang dapat dikatakan sebagai algoritma yang baik? Pada umumnya kita tidak ingin menggunakan algoritma yang salah untuk menyelesaikan masalah karena hal ini dapat menyebabkan masalah tidak diselesaikan dengan optimal, atau lebih buruknya, tidak diselesaikan sama sekali.
Sebuah algoritma yang baik memiliki sifat-sifat berikut:
- Benar, di mana algoritma menyelesaikan masalah dengan tepat, sesuai dengan definisi masukan / keluaran algoritma yang diberikan.
- Efisien, berarti algoritma menyelesaikan masalah tanpa memberatkan bagian lain dari apliikasi. Sebuah algoritma yang tidak efisien akan menggunakan sumber daya (memori, CPU) yang besar dan memberatkan aplikasi yang mengimplementasikan algoritma tersebut.
- Mudah diimplementasikan, artinya sebuah algoritma yang baik harus dapat dimengerti dengan mudah sehingga implementasi algoritma dapat dilakukan siapapun dengan pendidikan yang tepat, dalam waktu yang masuk akal.
Pembuktian Kebenaran Algoritma
Kita telah mengetahui bahwa sebuah algoritma yang baik adalah algoritma yang benar, efisien, dan mudah diimplementasikan. Pertanyaan berikutnya tentunya adalah, bagaimana kita mengetahui bahwa sebuah algoritma telah benar? Algoritma yang efisien itu seperti apa? Bagaimana kita mengukur kemudahan implementasi sebuah algoritma?
Bagian ini akan membahas mengenai pertanyaan pertama, yaitu bagaimana kita dapat mengetahui kebenaran sebuah algoritma. Tentunya efisiensi dan kemudahan implementasi sebuah algoritma menjadi tidak penting jika algoritma tersebut tidak dapat memberikan hasil yang benar.
Definisi dari kebenaran algoritma yang digunakan pada tulisan ini adalah sebagai berikut:
Pembuktian kebenaran sebuah algoritma sendiri dapat dilakukan dengan beberapa cara, misalnya:Sebuah algoritma dikatakan telah benar jika algoritma tersebut dapat memberikan keluaran yang benar jika menerima masukan sesuai dengan definisi algoritma tersebut, dan algoritma tersebut terbukti akan selalu dapat diterminasi (berakhir).
- Induksi Matematika,
- Pembuktian kontradiktif,
- Pembuktian kontrapositif, dan
- Metode Formal.
Sekarang mari kita lihat penggunaan masing-masing alat tersebut untuk membuktikan algoritma!
Induksi Matematika
Induksi matematika merupakan alat pembuktian matematis yang digunakan untuk membuktikan pernyataan atau proses yang melibatkan perhitungan bilangan asli yang berulang. Contoh dari rumus matematis yang dapat dibuktikan dengan menggunakan induksi matematika yaitu perhitungan deret aritmatika, deret geometris, ataupun sigma bilangan.
Pembuktian menggunakan induksi matematika dilakukan dengan dua langkah, yaitu:
- Melakukan pembuktian kasus dasar (base case), yaitu membuktikan bahwa sebuah pernyataan (fungsi) matematika atau algoritma bernilai benar jika diaplikasikan pada bilangan pertama yang sah sesuai dengan spesifikasi fungsi atau algoritma tersebut.
- Melakukan induksi, yaitu membuktikan bahwa kebenaran dari fungsi
P(k+1) jika kebenaran fungsiP(k) diketahui.
Untuk lebih jelasnya, mari kita lihat beberapa contoh cara pembuktian yang dilakukan dengan menggunakan induksi matematika.
Contoh 1: Deret Aritmatika
Misalkan kita diminta untuk membuktikan bahwa pernyataan matematika untuk perhitungan deret aritmatika berikut:
adalah benar untuk semua bilangan bulat1+2+3+...+n=n(n+1)2 n≥1 .
Untuk membuktikan pernyataan matematika di atas, terlebih dahulu kita harus mengubah pernyataan matematika tersebut menjadi sebuah fungsi matematika:
dan kemudian membuktikan kebenarannya menggunakan induksi matematika. Seperti yang telah dijelaskan sebelumnya, kita harus menjalankan dua langkah untuk melakukan pembuktian dengan induksi:P(k)=1+2+3+...+n=k(k+1)2
- Pembuktian Kasus DasarKarena pernyataan matematika pada soal menyatakan bahwa pernyataan benar untuk semua bilangan bulat
k≥1 , maka untuk pembuktian kasus dasar kita harus membuktikan bahwaP(1) adalah benar untuk ruas kiri maupun ruas kanan dariP(k) .
karena hasil akhir dari ruas kanan dan ruas kiri adalah sama (P(1)=1111=1(1+1)2=1(2)2=22=1 1 ), maka dapat dikatakan bahwa kasus dasar telah terbukti.
- InduksiUntuk pembuktian induksi, kita harus membuktikan bahwa
P(k)→P(k+1) bernilai benar.
Langkah pertama yang dapat kita lakukan yaitu menuliskan fungsi matematis dariP(k+1) terlebih dahulu:
dan kemudian kita harus membuktikan bahwa ruas kiri dan ruas kanan dariP(k+1)=1+2+...+k+(k+1)=(k+1)((k+1)+1)2 P(k+1) adalah sama. Pembuktian akan kita lakukan dengan melakukan penurunan pada ruas kiri agar menjadi sama dengan ruas kanan:
dan seperti yang dapat dilihat, ruas kiri dari1+2+...+k+(k+1)=(1+2+...+k)+(k+1)=k(k+1)2+(k+1)=k(k+1)+2(k+1)2=k2+3k+22=(k+1)(k+2)2=(k+1)((k+1)+2)2 P(k+1) telah menjadi sama dengan ruas kanannya, sehingga dapat dikatakan bahwa tahap induksi telah berhasil dibuktikan benar.
P(n) bernilai benar untukn≥1 .
Contoh 2: Pembuktian Hipotesa
Anda diminta untuk membuktikan hipotesa bahwa fungsi matematikan3−n habis dibagi 6 untuk semua bilangan bulatn≥2 .
Langkah untuk membuktikan pernyataan tersebut sama dengan sebelumnya. Mulai dari definisi ulang fungsi matematikanya:
Dan kemudian lakukan induksi matematika, langkah demi langkah:P(k)=k3−k
- Pembuktian Kasus DasarLakukan perhitungan
P(2) (karena nilaik minimal 2) dan pastikan hasilnya habis dibagi 6:
karenaP(1)=23−2=8−2=6 6mod6=0 maka telah dapat dibuktikan bahwa kasus dasar bernilai benar.
- InduksiJika
P(k) benar habis dibagi 6, makaP(k+1) , atau(k+1)3−(k+1) harus juga habis dibagi 6. Mari kita lakukan pembuktiannya:
dan dapat dilihat bagaimanaP(k+1)=(k+1)3−(k+1)=(k3+3k2+3k+1)−k−1=k3−3k2+2k=k3−3k2+2k+k−k=k3−3k2+3k−k=k3−k+3k2+3k=(k3−k)+3k(k+1) P(k+1) telah terbukti habis dibagi 6 karena:
k3−k habis dibagi 6, sesuai dengan hipotesaP(k) , dan3k(k+1) habis dibagi 6 karena salah satu nikai darik atauk+1 pasti merupakan bilangan genap, yang jika dikalikan dengan 3 akan habis dibagi 6.
P(k)=k3−k habis dibagi 6 untukk≥2 .
Induksi Matematika untuk Pembuktian Algoritma
Seperti yang dapat dilihat dari apa yang telah kita pelajari pada bagian sebelumnya, induksi matematika jelas sangat berguna untuk membuktikan kebenaran sebuah teorema atau fungsi yang melibatkan perhitungan bilangan bulat yang berulang. Tetapi apa guna induksi matematika untuk membuktikan kebenaran sebuah algoritma?
Sebuah algoritma kerap kali akan memiliki bagian yang melakukan perhitungan bilangan atau data secara berulang. Kita dapat menggunakan konsep perulangan pada pemrograman untuk menerapkan perhitungan bilangan ataupun data secara berulang. Misalnya, algoritma berikut menghitung hasil kali dari dua buah bilangan bulat:
yang secara matematis dapat dituliskan sebagai fungsi berikut:def kali(m, n): if m < 0: return -1 # error else: i = 0 result = 0 while(m != i): result = result + n i = i + 1 return result
atau lebih sederhananya:f(m,n)=∑i=1nm;n≥0
dan secara otomatis tentunya pernyataan matematis tersebut dapat kita buktikan dengan menggunakan induksi matematika. Pembuktian perulangan yang lebih kompleks sendiri dapat dilakukan dengan teknik yang dikenal dengan nama loop invariant, yang tidak akan dijelaskan pada tulisan ini.m×n=m+m+m+...+mn kali
Pemodelan Masalah
Pada bagian sebelumnya kita telah melihat bagaimana sebuah algoritma dituliskan menjadi fungsi matematika. Baik algoritma maupun fungsi matematika adalah sebuah model, yang digunakan untuk menggambarkan masalah yang ditemui pada dunia nyata, dan ingin diselesaikan, baik dengan menggunakan matematika ataupun program komputer. Dengan memiliki model masalah kita dapat lebih mudah mengerti masalah yang akan diselesaikan, yang akan menyebabkan solusi yang ditawarkan menjadi lebih baik.
Tetapi pertanyaannya tentunya adalah, bagaimana kita membuat model yang benar dari masalah-masalah yang ada? Bagian ini akan menjelaskan mengenai cara pembangunan model, baik secara matematis maupun algoritmik, yang benar.
Jenis-Jenis Model
Sebelum mulai membangun model permasalahan, tentunya kita terlebih dahulu harus mengetahui jenis-jenis model yang ada. Terdapat enam jenis model yang umum digunakan untuk menggambarkan masalah dalam dunia algoritma / pemrograman, yaitu:
- Model NumerikModel numerik merupakan model matematis yang paling sederhana, yang dibuat untuk mendeskripsikan jumlah atau ukuran dari sesuatu. Model numerik menggunakan angka (1, 2, 3, dst) untuk mendeskripsikan suatu hal. Misalkan gambar di bawah:
memberikan informasi sejumlah sapi yang ada di dalam kotak. Model numerik paling sederhana dan informatif yang dapat kita ambil dari gambar tersebut adalah ‘Lima ekor Sapi’ atau ‘Lima Sapi’.Model Numerik Sapi
- Model SimbolikJika kita mengembangkan model numerik lebih jauh, kita kemudian dapat menambahkan simbol-simbol baru untuk melakukan pemrosesan terhadap angka-angka yang ada pada model numerik. Terdapat empat buah simbol dasar untuk pemrosesan angka, yaitu
+,−,×,dan÷ . Simbol= juga digunakan untuk menandakan kesamaan nilai antara ruas kiri dan ruas kanan dari= .
Jadi, sebuah ekspresi matematika seperti ini:NoteSimbol×dan÷ akan dituliskan sebagai∗ dan/ pada tulisan ini, karena kedua simbol tersebut lebih umum digunakan pada lingkungan ilmu komputer.
dapat dikatakan adalah sebuah model simbolik. Tentunya operator-operator numerik yang disebutkan sebelumnya memiliki aturan tertentu untuk beropearsi. Aturan-aturan umum yang kita temui untuk operator numerik yaitu:10=5∗2
- Hukum Kumulatif, di mana
a+b=b+a dana∗b=b∗a . - Hukum Asosiatif, di mana
a+(b+c)=(a+b)+c dana∗(b∗c)=(a∗b)∗c . - Hukum Distribusi, di mana
a∗(b+c)=(a∗b)+(a∗c) . - Hukum Invers, yaitu
a+(−a)=0 dan a * frac{1}{a} = 1. - Hukum Identitas, yaitu
a+0=a$dan$a∗1=a . - Perkalian dengan 0, yaitu
a∗0=0 .
Sebuah variabel merupakan simbol yang digunakan untuk merepresentasikan nilai yang dapat berubah kapanpun, tergantung dari nilai yang kita berikan kepada variabel tersebut. Variabel digunakan dalam model simbolik untuk mewakili nilai-nilai yang dapat berubah sewaktu-waktu, misalnya nilai yang harus dibaca dari masukan pengguna atau nilai yang diambil secara acak. Sebuah model bahkan dapat terdiri dari hanya variabel saja, misalnya model matematika untuk menghitung luas sebuah persegi panjang dapat dituliskan seperti berikut:
di manaL=p∗l p danl mewakili panjang dan lebar persegi panjang, yang nilainya selalu berbeda-beda, tergantung dengan persegi panjang yang akan dihitung luasnya. NilaiL , yang merepersentasikan luas persegi panjang, sendiri bergantung kepada nilaip danl , sehingga kita tidak akan mendapatkan nilaiL yang konstan.
Deklarasi variabel sendiri dilakukan dengan menggunakan perintah $let$, seperti berikut:
Selain model-model dengan variabel, tentunya kita juga memiliki model-model yang memiliki bilangan konstan yang tidak berubah, misalnya untuk menghitung luas segitiga:let L=Luas Persegi
atau model untuk menghitung keliling lingkaran:L=12∗a∗t
Nilai-nilai yang tidak pernah berubah pada kedua model di atas (sepertiK=2∗π∗r 2 ,12 , danπ ) dikenal dengan nama konstanta. Perhatikan bahwa konstanta dapat mencakup angka “mentah” seperti2 ataupun simbol yang dikenal secara luas sepertiπ . Konstanta biasanya dideklarasikan pada awal model atau kamus data program, dan tidak pernah berubah nilainya selama model tersebut digunakan.
Dari berbagai komponen dan contoh model simbolik yang telah kita lihat, dapat disimpulkan bahwa model simbolik merupakan model yang menggambarkan interaksi dan operasi antar komponen numerik secara abstrak. Abstraksi dari komponen numerik (angka) pada model simbolik dilakukan dengan menggunakan variabel dan konstanta.
- Hukum Kumulatif, di mana
- Model SpasialTidak semua permasalahan yang diselesaikan oleh matematika atau komputer selalu berhubungan langsung dengan angka. Terkadang kita menjumpai juga masalah-masalah yang berhubungan dengan representasi dunia nyata seperti perhitungan jarak dua objek atau pencarian jalur terdekat untuk kendaraan. Secara tradisional, model untuk penyelesaian masalah seperti ini digambarkan dengan peta, graph, dan gambar-gambar teknis lainnya.
Untuk dunia komputer, model-model dunia nyata biasanya digambarkan dengan menggunakan koordinat. Sistem koordinat yang paling populer digunakan dalam hal ini adalah koordinat kartesius. Koordinat kartesius merupakan sistem koordinat yang menggambarkan sebuah nilai riil di dalam kumpulan nilai yang direpresentasikan dengan sebuah garis. Sistem kartesius dapat digambarkan dalam banyak dimensi, sesuai dengan jumlah kumpulan nilai yang digambarkan. Untuk memudahkan pengertian, gambar di bawah memperlihatkan contoh sistem koordinat kartesius dua dimensi:
Untuk menyederhanakan masalah, mayoritas algoritma dan solusi yang dikembangkan dalam kuliah ini akan dilakukan dengan menggunakan sistem kartesius dua dimensi. Sistem tiga dimensi dan satu dimensi dianggap dapat diimplementasikan menggunakan konsep yang sama dengan sistem dua dimensi.Sistem Koordinat Kartesius
Data pada sistem kartesius dua dimensi dapat direpresentasikan dalam bentuk sebuah titik, yaitu kombinasi antara sumbu x dan sumbu y:
atau sebuah garis, yang direpresentasikan dengan sebuah fungsi matematika:Titik pada Kartesius
Dalam prakteknya, kita juga akan sering memerlukan informasi arah pergerakan dari sebuah garis. Untuk merepresentasikan hal tersebut, kita dapat menambahkan sebuah tanda panah pada garis:Garis pada Kartesius
dan yang terakhir, kita dapat juga merepresentasikan sebuah bentuk atau bidang, menggunakan kombinasi beberapa garis:Garis Berarah pada Kartesius
Untuk melakukan pemrosesan data-data yang ada di dalam sistem kartesius, kita dapat melakukan operasi terhadap titik-titik yang merepresentasikan data tersebut. Titik-titik direpresentasikan dalam bentuk matriks atau array. Misalnya, segitiga yang ada pada gambar di atas dapat direperesentasikan sebagai matriks berikut:Bidang pada Kartesius
Dan kemudian tentunya kita dapat melakukan operasi-operasi matriks untuk melakukan berbagai hal terhadap segitiga tersebut.[−31431−2]
- Model LogisModel logis merupakan cara memodelkan masalah berdasarkan logika matematika. Terdapat empat cabang utama dari logika matematika, yaitu teori himpunan, teori model, teori rekursif, dan teori pembuktian. Masing-masing teori memiliki cara pemodelan yang berbeda-beda, untuk merepresentasikan masalah yang berbeda. Tulisan ini hanya akan membahas pemodelan logis pada bidang himpunan, dan relevansinya dengan salah satu sistem yang paling populer di dunia komputer: basis data.
Himpunan, seperti namanya, memodelkan sekumpulan entitas yang memiliki atribut (ciri khas) tertentu. Dalam menentukan atribut tujuan dari pengunaan himpunan lebih penting daripada kesamaan ciri khas dari entitas, sehingga terkadang atribut dari elemen-elemen dalam himpunan tidak selalu dapat dilihat dengan mudah. Misalnya, kita dapat mendeklarasikan sebuah himpunan dengan nama “Himpunan Barang dalam Handbag” dengan isi berupa “handphone, gunting kuku, alat make-up, tissue, dompet, alat tulis, dan karet gelang”. Secara sekilas semua entitas yang ada di dalam himpunan tidak terlihat memiliki atribut yang jelas, meskipun himpunan ini adalah himpunan yang valid.
Terdapat dua aturan khusus yang harus dipenuhi oleh sebuah himpunan, yaitu:
- Himpunan harus didefinisikan dengan tepat. Sebuah entitas yang ada di dunia hanya dapat memiliki dua status berkaitan dengan himpunan yang didefinisikan: TERMASUK dalam himpunan atau TIDAK TERMASUK. Tidak boleh ada elemen yang bersifat ambigu, dalam arti tidak jelas masuk ke dalam himpunan atau tidak. Misalnya, kita tidak dapat mendefinisikan sebuah himpunan yang berisi “Orang Tinggi” karena tidak terdapat definisi dari “tinggi” yang jelas. Apakah 170 cm termasuk tinggi? 180?Yang dapat kita definisikan ialah himpunan yang berisi “Orang dengan tinggi badan di atas 175 cm”, sehingga tidak terdapat perdebatan mengenai apakah 170 cm termasuk tinggi atau tidak.
- Setiap elemen dalam himpunan harus unik. Sebuah himpunan tidak boleh memiliki nilai ganda. Aturan ini menyebabkan banyak himpunan yang ada di dunia nyata tidak dapat direpresentasikan dengan himpunan matematika. Misalnya, kita dapat saja memiliki himpunan sendok yang terdiri dari banyak sendok identik. Dalam himpunan matematis, hal ini tidak diperbolehkan. Aturan ini juga menyebabkan penggabungan himpunan menjadi sedikit berbeda. Himpunan berisi angka 1, 2, 3, 4 jika digabungkan dengan himpunan 3, 4, 5, 6 akan menghasilkan himpunan 1, 2, 3, 4, 5, 6. Ide “nilai unik” untuk setiap elemen dalam himpunan ini lah yang menjadi dasar dari pengindeksan dan primary key dari basis data relasional.
Dari gambar diagram Venn di atas, kita dapat melihat bagaimana seluruh persegi adalah juga persegi panjang, dan baik persegi maupun persegi panjang adalah merupakan segi empat. Jika kita menambahkan jenis segi empat lainnya, misalnya trapesium, dapatkah anda menggambarkan diagram Venn-nya?Contoh Diagram Venn
- Model StatistikTerdapat banyak permasalahan di dunia nyata yang tidak dapat dimodelkan dengan mudah menggunakan keempat model matematis yang telah kita bahas sebelumnya. Terkadang kita dihadapkan dengan permasalahan yang sangat kompleks, sampai-sampai memodelkan dan menganalisa setiap situasi yang mempengaruhi masalah tersebut akan menjadi sangat mahal, memerlukan banyak orang, dan banyak waktu.
Sebagai contoh, bayangkan jika kita diminta untuk melakukan prakiraan cuaca. Dengan menggunakan model matematis yang ada, kita akan memerlukan sangat banyak kalkulasi, yang saling mempengaruhi satu sama lainnya. Praktisnya, kita harus mampu melakukan simulasi terhadap seluruh elemen yang ada di bumi untuk melakukan prakiraan cuaca dengan tepat. Hal ini tentunya sangat tidak efektif untuk dilakukan. Lalu bagaimana para ahli sekarang melakukan prakiraan cuaca?
Jawabannya adalah model statistik. Dengan mengumpulkan sampel data cuaca pada masa lalu, kita dapat melihat kecenderungan atau tren cuaca yang akan terjadi sesuai dengan keadaan cuaca kita sekarang. Pada dasarnya, sebuah model statistik melakukan analisa tren terhadap sampel data yang relevan untuk meniadakan ketidak pastian atau keadaan khusus. Dengan mengambil keadaan rata-rata dari sekumpulan data, kita akan mendapatkan kecenderungan dari sebuah keadaan jika dihadapkan dengan keadaan umumnya.
Gambar di atas menunjukkan contoh dari model statistik. Ingat, bahwa kesimpulan yang dapat diambil dari sebuah model statistik hanyalah berupa kecenderungan atau tren. Kita tidak bisa membuktikan sesuatu atau memberikan hasil yang pasti menggunakan statistik. Dapat dikatakan bahwa kalimat seperti “statistik membuktikan ...” pada tulisan ilmiah populer kurang tepat.Contoh Model Statistik
- PseudocodeSemua model matematis yang telah dijelaskan sebelumnya merupakan model matematika yang digunakan dan dimengerti oleh manusia. Jika ingin menggunakan model matematis tersebut di komputer, terlebih dahulu kita harus melakukan konversi menjadi kode program yang dapat dibaca dan dimengerti oleh komputer. Kode program sendiri dimodelkan dengan banyak cara, dan yang paling relevan dengan algoritma ialah pseudocode.
Pseudocode memberikan langkah-langkah penyelesaian masalah dengan menggunakan bahasa manusia, dengan sedikit batasan sesuai dengan konstruk logika komputer. Pseudocode tidak memiliki konstruk untuk bahasa pemrograman tertentu, sehingga pseudocode harus bisa diimplementasikan dengan bahasa pemrograman apapun. Berikut adalah contoh pseudocode sederhana:
Untuk penjelasan lebih mendetail tentang pseudocode, silahkan baca kembali bahan kuliah untuk Pemrograman Dasar.for i = 1 to 5 do print i end for
Pengembangan Model
Proses pengembangan model dapat dilakukan dengan beberapa langkah yang telah dibangun oleh para ahli matematika. Jika proses pengembangan model dilakukan mengikuti langkah-langkah yang ada, idealnya kita akan mendapatkan model yang tepat untuk permasalahan yang akan diselesaikan. Adapun langkah-langkah yang harus diambil untuk membangun sebuah model yaitu:
- Apakah masalah yang dihadapi merupakan masalah yang memerlukan solusi matematis? Jika masalahnya merupakan masalah numerik (perhitungan angka) atau logis, maka jawabannya sudah pasti “ya”. Jika solusi dari masalah berupa pendapat, maka kemungkinan jawabannya adalah “tidak”.
- Fakta-fakta relevan apa saja yang diketahui? Masalah umum yang dihadapi saat akan membangun solusi adalah informasi yang terlalu banyak, yang terkadang mencuri fokus kita dari akar masalah. Pisahkan antara fakta (informasi) yang relevan dari keseluruhan informasi yang didapatkan.
- Fakta atau informasi tambahan apa yang kita perlukan untuk menyelesaikan masalah? Di mana atau bagaimana cara agar kita mendapatkan fakta-fakta tersebut?
- Adakah langkah atau metode alami untuk menyelesaikan masalahnya? Metode alami artinya metode yang umumnya digunakan oleh manusia. Misalnya, untuk menghitung total dari sekumpulan nilai kita dapat menambahkan seluruh bilangan yang ada di dalam kumpulan nilai tersebut.
- Apakah fakta-fakta yang ada dapat direpresentasikan oleh simbol matematis dan dikategorikan menjadi fakta yang “diketahui” dan “tidak diketahui”?
- Apakah terdapat model lama yang dapat digunakan atau disesuaikan untuk menyelesaikan masalah kita?
- Jika terdapat model yang telah dikembangkan sebelumnya untuk masalah kita, apakah model tersebut dapat diaplikasikan pada komputer?
- Bagaimana kita dapat mengaplikasikan model dari solusi kita sehingga model tersebut dapat dibuat menjadi program komputer dengan mudah?
Contoh: Perhitungan Bunga Pinjaman
Kita diminta untuk mengembangkan sebuah program komputer untuk sebuah perusahaan kredit ACME. Program yang akan kita kembangkan merupakan sistem untuk menghitung total jumlah yang harus dibayar oleh peminjam uang per tahunnya. Bunga pinjaman yang diberikan ACME adalah sebesar 15% per tahunnya.
Untuk membangun sistem perhitungan yang diminta, tentunya terlebih dahulu kita harus membangun modal solusi untuk perhitungan bunganya. Mari kita ikuti langkah-langkah untuk membangun model yang telah dijelaskan sebelumnya:
- Apakah masalah yang dihadapi merupakan masalah yang memerlukan solusi matematis?Ya. Perhitungan total bunga bunga jelas akan melibatkan matematika.
- Fakta-fakta relevan apa saja yang diketahui?Bunga pinjaman sebesar 15% per tahun.
- Fakta atau informasi tambahan apa yang kita perlukan untuk menyelesaikan masalah?Beberapa fakta tambahan yang harus ada tetapi tidak disebutkan secara eksplisit pada deskripsi masalah:
- Jumlah pinjaman awal. Untuk menghitung total pinjaman dengan bunganya jelas kita harus mengetahui jumlah pinjaman awal terlebih dahulu.
- Lama pinjaman. Tanpa adanya lama pinjaman, kita tidak dapat mengetahui dengan pasti total bunga yang harus ditambahkan.
- Adakah langkah atau metode alami untuk menyelesaikan masalahnya?Ya, lakukan perhitungan bunga tiap tahunnya, dan tambahkan hasil kalkulasi tersebut sampai tahun pinjaman terakhir.
- Apakah fakta-fakta yang ada dapat direpresentasikan oleh simbol matematis?Dari fakta-fakta yang kita dapatkan pada langkah kedua dan ketiga, kita dapat mendefinisikan simbol matematis seperti berikut:
let blet plet tlet T=bunga=jumlah pinjaman=waktu pinjaman (per tahun)=total pinjaman - Apakah terdapat model lama yang dapat digunakan untuk menyelesaikan masalah kita?Ya, perhitungan bunga majemuk yang dimodelkan dengan rumus:
T=p(1+b)t .
- Apakah model yang ada sebelumnya pada langkah 6 dapat diaplikasikan pada komputer?Kemungkinan tidak, karena perhitungan bunga majemuk merupakan perhitungan yang tidak banyak diketahui orang (terutama pada bidang pemrograman), dan juga memiliki banyak aturan kompleks yang harus dimengerti terlebih dahulu.
Karena kasus yang sederhana, kita akan lebih mudah mengimplementasikan algoritma kita sendiri, yang cukup melakukan iterasi dan menambahkan total pinjaman setiap tahunnya. Mari kita coba kembangkan model iterasi yang dapat digunakan.
Untuk tahun pertama, peminjam akan berhutang sebanyak:
selanjutnya, untuk tahun kedua hutangnya akan bertambah menjadi:T=p+(15%∗p)
di manaT′=T+(15%∗T) T′ adalah nilai baru dariT . Kita cukup melakukan perhitungan yang sama terus menerus, sebanyak $t$ kali untuk mendapatkan hasil akhir berupaT yang menyimpan total hutang yang dipinjam. Jika dikembangkan, maka model matematis akhir yang kita dapatkan adalah:
yang akan dijalankan sebanyak $t$ kali, dengan nilai $T$ yang bertambah setiap iterasinya. Dengan informasi ini, kita dapat mengimplementasikan pseudocode seperti berikut:T=T+(15100∗T)
yang kemudian akan kita implementasikan sebagai fungsi penghitung total pinjaman.b = 15 T = 0 READ p, t T = p for i = 1 to t do T = T + (15 / 100 * T) end for WRITE T
- Bagaimana kita dapat mengaplikasikan model dari solusi kita sehingga model tersebut dapat dibuat menjadi program komputer dengan mudah?Pseudocode yang ada sudah sangat jelas, dan baris per barisnya dapat diimplementasikan secara langsung menggunakan bahasa pemrograman apapun.
b = 15 T = 0 p = input("Masukkan jumlah pinjaman: ") t = input("Masukkan lama pinjaman: ") T = int(p) for i in range(1, int(t)): T = T + (15 / 100 * T) print("Total pinjaman yang harus dibayarkan adalah: " + str(T))
Kesimpulan
Pada bagian ini kita telah mempelajari tentang ciri khas algoritma yang baik, yaitu benar, efisien, dan mudah diimplementasikan. Kita juga mempelajari bagaimana membuktikan sebuah algoritma adalah sebuah algoritma yang benar, dan bagaimana mengembangkan algoritma yang benar, menggunakan model matematis.
Terdapat enam jenis model matematis yang kita bahas, beserta dengan cara menggunakan model matematis tersebut ke kasus pada dunia nyata. Selanjutnya kita akan mempelajari bagaimana mengembangkan algoritma yang efisien, beserta definisi dari efisiensi algoritma tentunya.
Komputer
1. Apakah Itu Algoritma
Ditinjau dari asal-usul katanya, kata Algoritma sendiri mempunyai sejarah yang aneh. Orang hanya menemukan kata algorism yang berarti proses menghitung dengan angka arab. Anda dikatakan algorist jika Anda menghitung menggunakan angka arab. Para ahli bahasa berusaha menemukan asal kata ini namun hasilnya kurang memuaskan. Akhirnya para ahli sejarah matematika menemukan asal kata tersebut yang berasal dari nama penulis buku arab yang terkenal yaitu Abu Ja’far Muhammad Ibnu Musa Al-Khuwarizmi. Al-Khuwarizmi dibaca orang barat menjadi Algorism. Al-Khuwarizmi menulis buku yang berjudul Kitab Al Jabar Wal-Muqabala yang artinya “Buku pemugaran dan pengurangan” (The book of restoration and reduction). Dari judul buku itu kita juga memperoleh akar kata “Aljabar” (Algebra). Perubahan kata dari algorism menjadi algorithm muncul karena kata algorism sering dikelirukan dengan arithmetic, sehingga akhiran –sm berubah menjadi –thm. Karena perhitungan dengan angka Arab sudah menjadi hal yang biasa, maka lambat laun kata algorithm berangsur-angsur dipakai sebagai metode perhitungan (komputasi) secara umum, sehingga kehilangan makna kata aslinya. Dalam bahasa Indonesia, kata algorithm diserap menjadi algoritma.
2. Definisi Algoritma
“Algoritma adalah urutan langkah-langkah logis penyelesaian masalah yang disusun secara sistematis dan logis”. Kata logis merupakan kata kunci dalam algoritma. Langkah-langkah dalam algoritma harus logis dan harus dapat ditentukan bernilai salah atau benar. Dalam beberapa konteks, algoritma adalah spesifikasi urutan langkah untuk melakukan pekerjaan tertentu. Pertimbangan dalam pemilihan algoritma adalah, pertama, algoritma haruslah benar. Artinya algoritma akan memberikan keluaran yang dikehendaki dari sejumlah masukan yang diberikan. Tidak peduli sebagus apapun algoritma, kalau memberikan keluaran yang salah, pastilah algoritma tersebut bukanlah algoritma yang baik.
Pertimbangan kedua yang harus diperhatikan adalah kita harus mengetahui seberapa baik hasil yang dicapai oleh algoritma tersebut. Hal ini penting terutama pada algoritma untuk menyelesaikan masalah yang memerlukan aproksimasi hasil (hasil yang hanya berupa pendekatan). Algoritma yang baik harus mampu memberikan hasil yang sedekat mungkin dengan nilai yang sebenarnya.
Ketiga adalah efisiensi algoritma. Efisiensi algoritma dapat ditinjau dari 2 hal yaitu efisiensi waktu dan memori. Meskipun algoritma memberikan keluaran yang benar (paling mendekati), tetapi jika kita harus menunggu berjam-jam untuk mendapatkan keluarannya, algoritma tersebut biasanya tidak akan dipakai, setiap orang menginginkan keluaran yang cepat. Begitu juga dengan memori, semakin besar memori yang terpakai maka semakin buruklah algoritma tersebut. Dalam kenyataannya, setiap orang bisa membuat algoritma yang berbeda untuk menyelesaikan suatu permasalahan, walaupun terjadi perbedaan dalam menyusun algoritma, tentunya kita mengharapkan keluaran yang sama. Jika terjadi demikian, carilah algoritma yang paling efisien dan cepat.
3. Beda Algoritma dan Program
Program adalah kumpulan pernyataan komputer, sedangkan metode dan tahapan sistematis dalam program adalah algoritma. Program ditulis dengan menggunakan bahasa pemrograman. Jadi bisa disebut bahwa program adalah suatu implementasi dari bahasa pemrograman. Beberapa pakar memberi formula bahwa :
Program = Algoritma + Bahasa (Struktur Data)
Bagaimanapun juga struktur data dan algoritma berhubungan sangat erat
pada sebuah program. Algoritma yang baik tanpa pemilihan struktur data
yang tepat akan membuat program menjadi kurang baik, demikian juga
sebaliknya.Pembuatan algoritma mempunyai banyak keuntungan di antaranya :
Untuk mengetahui dibutuhkannya pendeklarasian variabel dalam penggunaan bahasa pemrograman apabila tidak semua bahasa pemrograman membutuhkannya.
b. Pemilihan tipe data
Apabila bahasa pemrograman yang akan digunakan membutuhkan pendeklarasian variabel maka perlu hal ini dipertimbangkan pada saat pemilihan tipe data.
c. Pemakaian instruksi-instruksi
Beberapa instruksi mempunyai kegunaan yang sama tetapi masing-masing memiliki kelebihan dan kekurangan yang berbeda.
d. Aturan sintaksis
Pada saat menuliskan program kita terikat dengan aturan sintaksis dalam bahasa pemrograman yang akan digunakan.
e. Tampilan hasil
Pada saat membuat algoritma kita tidak memikirkan tampilan hasil yang akan disajikan. Hal-hal teknis ini diperhatikan ketika mengkonversikannya menjadi program.
f. Cara pengoperasian compiler atau interpreter.
Bahasa pemrograman yang digunakan termasuk dalam kelompok compiler atau interpreter.
4. Algoritma Merupakan Jantung Ilmu Informatika
Algoritma adalah jantung ilmu komputer atau informatika. Banyak cabang ilmu komputer yang mengarah ke dalam terminologi algoritma. Namun, jangan beranggapan algoritma selalu identik dengan ilmu komputer saja. Dalam kehidupan sehari-hari pun banyak terdapat proses yang dinyatakan dalam suatu algoritma. Cara-cara membuat kue atau masakan yang dinyatakan dalam suatu resep juga dapat disebut sebagai algoritma. Pada setiap resep selalu ada urutan langkah-langkah membuat masakan. Bila langkah-langkahnya tidak logis, tidak dapat dihasilkan masakan yang diinginkan. Ibu-ibu yang mencoba suatu resep masakan akan membaca satu per satu langkah-langkah pembuatannya lalu ia mengerjakan proses sesuai yang ia baca. Secara umum, pihak (benda) yang mengerjakan proses disebut pemroses (processor). Pemroses tersebut dapat berupa manusia, komputer, robot atau alat-alat elektronik lainnya. Pemroses melakukan suatu proses dengan melaksanakan atau “mengeksekusi” algoritma yang menjabarkan proses tersebut.
Algoritma adalah deskripsi dari suatu pola tingkah laku yang dinyatakan secara primitif yaitu aksi-aksi yang didefenisikan sebelumnya dan diberi nama, dan diasumsikan sebelumnya bahwa aksi-aksi tersebut dapat kerjakan sehingga dapat menyebabkan kejadian.
Melaksanakan algoritma berarti mengerjakan langkah-langkah di dalam algoritma tersebut. Pemroses mengerjakan proses sesuai dengan algoritma yang diberikan kepadanya. Juru masak membuat kue berdasarkan resep yang diberikan kepadanya, pianis memainkan lagu berdasarkan papan not balok. Karena itu suatu algoritma harus dinyatakan dalam bentuk yang dapat dimengerti oleh pemroses. Jadi suatu pemroses harus:
Komputer hanyalah salah satu pemroses. Agar dapat dilaksanakan oleh komputer, algoritma harus ditulis dalam notasi bahasa pemrograman sehingga dinamakan program. Jadi program adalah perwujudan atau implementasi teknis algoritma yang ditulis dalam bahasa pemrograman tertentu sehingga dapat dilaksanakan oleh komputer.
Kata “algoritma” dan “program” seringkali dipertukarkan dalam penggunaannya. Misalnya ada orang yang berkata seperti ini: “program pengurutan data menggunakan algoritma selection sort”. Atau pertanyaan seperti ini: “bagaimana algoritma dan program menggambarkan grafik tersebut?”. Jika Anda sudah memahami pengertian algoritma yang sudah disebutkan sebelum ini, Anda dapat membedakan arti kata algoritma dan program. Algoritma adalah langkah-langkah penyelesaikan masalah, sedangkan program adalah realisasi algoritma dalam bahasa pemrograman. Program ditulis dalam salah satu bahasa pemrograman dan kegiatan membuat program disebut pemrograman (programming). Orang yang menulis program disebut pemrogram (programmer). Tiap-tiap langkah di dalam program disebut pernyataan atau instruksi. Jadi, program tersusun atas sederetan instruksi. Bila suatu instruksi dilaksanakan, maka operasi-operasi yang bersesuaian dengan instruksi tersebut dikerjakan komputer.
Secara garis besar komputer tersusun atas empat komponen utama yaitu, piranti masukan, piranti keluaran, unit pemroses utama, dan memori. Unit pemroses utama (Central Processing Unit – CPU) adalah “otak” komputer, yang berfungsi mengerjakan operasi-operasi dasar seperti operasi perbandingan, operasi perhitungan, operasi membaca, dan operasi menulis. Memori adalah komponen yang berfungsi menyimpan atau mengingatingat.
Yang disimpan di dalam memori adalah program (berisi operasi-operasi yang akan dikerjakan oleh CPU) dan data atau informasi (sesuatu yang diolah oleh operasi-operasi). Piranti masukan dan keluaran (I/O devices) adalah alat yang memasukkan data atau program ke dalam memori, dan alat yang digunakan komputer untuk mengkomunikasikan hasil-hasil aktivitasnya. Contoh piranti masukan antara lain, papan kunci (keyboard), pemindai (scanner), dan cakram (disk). Contoh piranti keluaran adalah, layar peraga (monitor), pencetak (printer), dan cakram.
Mekanisme kerja keempat komponen di atas dapat dijelaskan sebagai berikut. Mula-mula program dimasukkan ke dalam memori komputer. Ketika program dilaksanakan (execute), setiap instruksi yang telah tersimpan di dalam memori dikirim ke CPU. CPU mengerjakan operasioperasi yang bersesuaian dengan instruksi tersebut. Bila suatu operasi memerlukan data, data dibaca dari piranti masukan, disimpan di dalam memori lalu dikirim ke CPU untuk operasi yang memerlukannya tadi. Bila proses menghasilkan keluaran atau informasi, keluaran disimpan ke dalam memori, lalu memori menuliskan keluaran tadi ke piranti keluaran (misalnya dengan menampilkannya di layar monitor).
6. Belajar Memprogram dan Belajar Bahasa Pemrograman
Belajar memprogram tidak sama dengan belajar bahasa pemrograman. Belajar memprogram adalah belajar tentang metodologi pemecahan masalah, kemudian menuangkannya dalam suatu notasi tertentu yang mudah dibaca dan dipahami. Sedangkan belajar bahasa pemrograman berarti belajar memakai suatu bahasa aturan-aturan tata bahasanya, pernyataan-pernyataannya, tata cara pengoperasian compiler-nya, dan memanfaatkan pernyataan-pernyataan tersebut untuk membuat program yang ditulis hanya dalam bahasa itu saja. Sampai saat ini terdapat puluhan bahasa pemrogram, antara lain bahasa rakitan (assembly), Fortran, Cobol, Ada, PL/I, Algol, Pascal, C, C++, Basic, Prolog, LISP, PRG, bahasabahasa simulasi seperti CSMP, Simscript, GPSS, Dinamo. Berdasarkan terapannya, bahasa pemrograman dapat digolongkan atas dua kelompok besar :
7. Menilai Sebuah Algoritma
Ketika manusia berusaha memecahkan masalah, metode atau teknik yang digunakan untuk memecahkan masalah itu ada kemungkinan bisa banyak (tidak hanya satu). Dan kita memilih mana yang terbaik di antara teknikteknik itu. Hal ini sama juga dengan algoritma, yang memungkinkan suatu permasalahan dipecahkan dengan metode dan logika yang berlainan. Yang menjadi pertanyaan adalah bagaimana mengukur mana algoritma yang terbaik?. Beberapa persyaratan untuk menjadi algoritma yang baik adalah :
Instruksi di atas terdapat keraguan.
Instruksi di atas tidak efektif, agar efektif instruksi tersebut diubah.
Misal : Hitung akar 2 sampai lima digit di belakang koma.
8. Penyajian Algoritma
Penyajian algoritma secara garis besar bisa dalam 2 bentuk penyajian yaitu tulisan dan gambar. Algoritma yang disajikan dengan tulisan yaitu dengan struktur bahasa tertentu (misalnya bahasa Indonesia atau bahasa Inggris) dan pseudocode. Pseudocode adalah kode yang mirip dengan kode pemrograman yang sebenarnya seperti Pascal, atau C, sehingga lebih tepat digunakan untuk menggambarkan algoritma yang akan dikomunikasikan kepada pemrogram. Sedangkan algoritma disajikan dengan gambar, misalnya dengan flowchart. Secara umum, pseudocode mengekspresikan ide-ide secara informal dalam proses penyusunan algoritma. Salah satu cara untuk menghasilkan kode pseudo adalah dengan meregangkan aturan-aturan bahasa formal yang dengannya versi akhir dari algoritma akan diekspresikan. Pendekatan ini umumnya digunakan ketika bahasa pemrograman yang akan digunakan telah diketahui sejak awal.
Flowchart merupakan gambar atau bagan yang memperlihatkan urutan dan hubungan antar proses beserta pernyataannya. Gambaran ini dinyatakan dengan simbol. Dengan demikian setiap simbol menggambarkan proses tertentu. Sedangkan antara proses digambarkan dengan garis penghubung. Dengan menggunakan flowchart akan memudahkan kita untuk melakukan pengecekan bagian-bagian yang terlupakan dalam analisis masalah. Di
samping itu flowchart juga berguna sebagai fasilitas untuk berkomunikasi antara pemrogram yang bekerja dalam tim suatu proyek.
Ada dua macam flowchart yang menggambarkan proses dengan komputer, yaitu :
Kaidah-Kaidah Umum Pembuatan Flowchart Program
Dalam pembuatan flowchart Program tidak ada rumus atau patokan yang bersifat mutlak. Karena flowchart merupakan gambaran hasil pemikiran dalam menganalisis suatu masalah dengan komputer. Sehingga flowchart yang dihasilkan dapat bervariasi antara satu pemrogram dengan yang lainnya. Namun secara garis besar setiap pengolahan selalu terdiri atas 3 bagian utama, yaitu :
Untuk memahami lebih dalam mengenai flowchart ini, akan diambil sebuah kasus sederhana.
Kasus : Buatlah sebuah rancangan program dengan menggunakan flowchart, mencari luas persegi panjang.
Solusi : Perumusan untuk mencari luas persegi panjang adalah :
L = p . l
di mana, L adalah Luas persegi panjang, p adalah panjang persegi, dan l adalah lebar persegi. Keterangan :
Keterangan :Algoritma berisi langkah-langkah penyelesaian suatu masalah. Langkah-langkah tersebut dapat berupa runtunan aksi (sequence), pemilihan aksi (selection), pengulangan aksi (iteration) atau kombinasi dari ketiganya. Jadi struktur dasar pembangunan algoritma ada tiga, yaitu:
Dalam Algoritma, tidak dipakai simbol-simbol / sintaks dari suatu bahasa pemrograman tertentu, melainkan bersifat umum dan tidak tergantung pada suatu bahasa pemrograman apapun juga. Notasi-notasi algoritma dapat digunakan untuk seluruh bahasa pemrograman manapun.
Definisi Pseudo-code
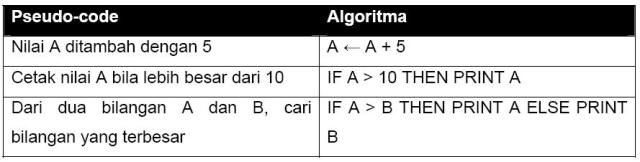
Kode atau tanda yang menyerupai (pseudo) atau merupakan penjelasan cara menyelesaikan suatu masalah. Pseudo-code sering digunakan oleh manusia untuk menuliskan algoritma.
Contoh kasus : mencari bilangan terbesar dari dua bilangan yang diinputkan
Solusi Pseudo-code :
10. Tahapan dalam Pemrograman
Langkah-langkah yang dilakukan dalam menyelesaikan masalah dalam pemrograman dengan komputer adalah :
Top 5 Popular of The Week
-
Algoritma dan Pemrograman 1. Apakah Itu Algoritma Ditinjau dari asal-usul katanya, kata Algoritma sendir...
-
Cara sederhana ,.. Yang biasa ane gunakan untuk shading dalam membuat digipaint Jangan tanya ini gambar apa,.. pacman emotikon pacman...
-
CPU mengeluarkan suara Beep beberapa kali dan tidak ada tampilan ke layar monitor, padahal monitor tidak bermasalah . Bunyi Beep menandaka...
-
karya : Togu Parasian Nainggolan karya: Zi zuan karya : zi zuan karya: Andrew Part II